小学生高学年算数 速さの安直な教え方「みはじ」計算

たとえば、
「30分に3000m歩く人の速さは分速何メートルですか。」
という問題があるとき、「速さ=道のり÷時間」という公式を知っていれば、3000÷30=100で答え 分速100mと答えを出せます。
また、
「分速100mで歩く人は30分で歩く道のりは何メートルですか。」
ならば、「道のり=速さ×時間」から3000m
さらに、「分速100mで歩く人は3000mを何分で歩くでしょうか。」
ならば、「時間=道のり÷速さ」から30分となります。
この3つの式を憶えるのに安直な教え方が昔からあります。「みはじ」計算です。
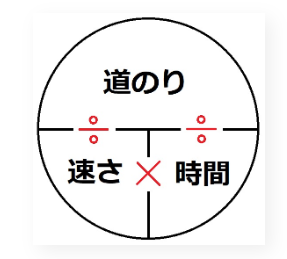
これは便利なので(=速さ以外でも使えるので)憶えておくべきです。念のため使い方を説明します。利用法が分からなければ話になりませんから。
①知りたいところを隠します。
②残りの式で解きます。(例:「道のり」を隠すと、「速さ」×「時間」)、「速さ」を隠すと、「道のり」÷「時間」)
通常は、「道のり」は「み」、「速さ」は「は」、「時間」は「じ」と略し、赤字の÷も×も書きません。横どうしは掛け算、上下は割り算と覚えておきます。〇を書いて、Tを書いて、上に「み」、下に「は」と「じ」と書けばいいのです。下は逆でも問題ないので、「〇Tみ」だけ思えておけばOKです。
これを、「距離=き」なので「きはじ」「はじき」と憶えさせたり、漢字の勉強を兼ねて「距速時」、英語の勉強を兼ねて「DST」(Distance,Speed,Time)と覚えさせる方法もあります。
ただし、これだけ覚えても問題を解くのは簡単ではありません。
みはじ計算だけでは算数の力を伸ばせない
小学校学習指導要領には、5年の指導内容として「速さなど単位量当たりの大きさの意味及び表し方について理解」させるとあります。
すなわち、「速さ」とは「単位量」=1分・1時間・1秒当たりにどれだけ移動するかという大きさということになります。
1分当りに進む道のりならば分速、1時間当りに進む道のりならば時速、1秒当りに進む道のりならば秒速ということです。日速とか年速という言葉はありませんが、単位量当たりの大きさということが分かっていれば解けます。
テストに出てくる問題は、速さの意味が分からないと「みはじ」だけでは解けない文章題が多いように思います。
「1時間に6km歩く人の速さは分速何メートルですか。」
という問題に出会ったとき、「みはじ」で6÷1=6として「答え 6m」ではいけませんね。6kmは1時間あたりに進んだ道のりなので、分速すなわち1分当りに直さなければいけません。また、求める単位は「m」なので、mに直す必要があります。
すなわち、「6km」は「6000m」に、「1時間」は「60分」に直して、6000÷60=100となり100mが正解となります。
算数の問題を常識で解く

わたしはよく子どもに「答えを常識で見直そう」と言います。上記の問題で出た答えが「分速6m」と出たとき、「1分間で6mしか進まないのはおかしい。」という常識を持ち合わせていれば、考え直すことができるはずです。
しかし、簡単に大人は「常識」と言いますが、その常識を学ぶのが小学生とも言えるのです。学校だけでなく家庭でも日常生活の中で「1分」という時間は実感で体得してほしいものです。また、意外に分かっていないのが距離感覚です。1mや100mくらいは授業や学校での体育などでつかめていますが、1km、100kmとなると怪しくなります。
家から学校までとか、ちょうど1km、約1kmが自分の住んでいるところからどの辺までなのか、地図や実体験で知っておくようにしましょう。速さについても、1時間か1km歩いてみたり、車での時速100kmでどこまで行けるかなどの体験は重要です。
これは、重さ、面積、体積の単位量についても言えることです。
みはじ計算の応用
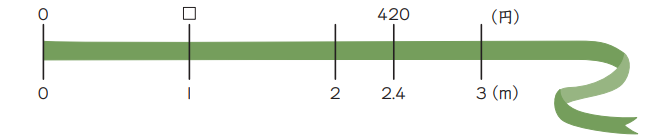
「速さなど」とあるように「単位量当たりの大きさ」の考え方は、他にも使えます。
「リボンを2.4m買うと, 代金は420円でした。このリボン1mのねだんは何円ですか。」
420÷2.4ですが、「み」を代金、「は」を1mの値段、「じ」を長さと置き換え可能です。
6年算数・中1数学の比・反比例の学習につながる学習
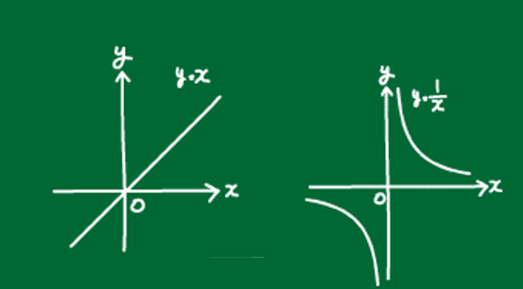
「単位量当たりの大きさ」という考え方、または「みはじ」の考え方は、6年算数・中1数学の比・反比例の学習につながる学習となっています。
すなわち、速さを一定にして時間を2倍3倍にすると進む道のりも2倍3倍となり、時間を一定にして速さを2倍3倍にすると道のりも2倍3倍となります。これが比例です。
「1mの値段を一定にして長さを2倍3倍にすると代金も2倍3倍となり、長さを一定にして1mの値段を2倍3倍にすると代金も2倍3倍となる。」でも同様に比例です。
また、道のりを一定にして速さを2倍3倍にするとかかる時間は1/2倍,1/3倍となり、道のりを一定にしてかける時間を2倍3倍にすれば速さ1/2倍,1/3倍となります。これが反比例です。
代金を一定にして1mの値段をを2倍3倍にすると長さは1/2倍,1/3倍となり、代金を一定にして長さを2倍3倍にすると1mの値段は1/2倍,1/3倍となります。これも反比例です。